| ¬¬A A A | снятие двойного отрицания |
| ¬(SaP&SaP´) | |
| ¬(SaS´ & S´aS) | |
| ¬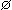 i i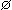 | |
| ¬A (A (A B) B) | закон противоречия |
| ¬SaP | |
| ¬SaP SoP SoP | |
| ¬SaS´ | |
| ¬SeP | |
| ¬SeP SiP SiP | |
| ¬SeS | |
| ¬SiP | |
| ¬SiP SeP SeP | |
| ¬SiS´ | |
| ¬SiS  SaP SaP | |
| ¬SoP | |
| ¬f | закон непротиворечия |
| þA  A A | формализация аксиомы Спинозы: Idea vera debet cum suo ideato convenire (Истинная идея должна быть согласна с своим объектом) |
| (¬SaP & SiS)  SoP SoP | |
| (¬SiP & SiS)  SeP SeP | |
| ((A B)&(B B)&(B A)) A)) (A (A B) B) | |
| (A&B) A A | исключение конъюнкции |
| (A&B) B B | исключение конъюнкции |
| (A B) B) ((A ((A B)&(B B)&(B A)) A)) | |
| (A ((B ((B B) B) A)) A)) (((A (((A B) B) B) B) ((B ((B A) A) A)) A)) | |
| (A ((B ((B C) C) D)) D)) ((B ((B C) C) (A (A D)) D)) | |
| (A (A (A B)) B)) (A (A B) B) | |
| (A (B (B C)) C)) ((A ((A B) B) (A (A C)) C)) | самодистрибутивность импликации |
| (A (B (B C)) C)) (B (B (A (A C)) C)) | |
| (A A) A) (((((A (((((A B) B) B) B) A) A) C) C) (((((B (((((B A) A) A) A) B) B) C) C) C)) C)) | |
| (A B) B) ((A ((A ¬B) ¬B) ¬A) ¬A) | |
| (A B) B) (C (C (A (A B)) B)) | |
| (A C) C) ((B ((B C) C) ((A ((A B) B) C)) C)) | |
| (B C) C) ((A ((A B) B) (A (A C)) C)) | |
| (M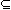 S & M S & M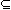 P) P)  M M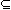 (S (S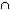 P) P) | |
| (MaP & MiS)  SiP SiP | |
| (MaS & MaP)  Ma(S Ma(S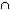 P) P) | |
| (MeP&SaM) SaP´ SaP´ | |
| (MeP&SiM) SiP´ SiP´ | |
| (P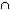 P´) P´)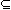 S S | |
| (S M & M M & M P) P)  S S P P | |
| (S M & MaP) M & MaP)  S S P P | |
| (S P & P P & P P) P)  P P S S | |
| (S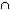 (P (P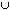 M)) M))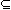 ((S ((S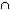 P) P)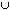 (S (S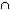 M)) M)) | |
| (S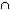 P)´ P)´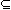 (S´ (S´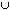 P´) P´) | |
| (S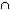 P)eM P)eM  (M (M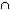 S)eP S)eP | |
| (S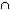 P)iM P)iM  SiP SiP | |
| (S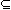 M & M M & M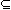 P) P)  S S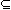 P P | |
| (S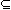 M & P M & P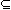 M) M)  (S (S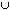 P) P)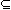 M M | |
| (S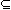 P & P P & P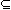 S) S)  S=P S=P | |
| (S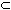 M & M M & M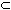 P) P)  S S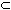 P P | транзитивность строгого включения |
| (S=M & M=P)  S=P S=P | |
| (SaM & MaP)  SaP SaP | модус barbara |
| (SaM & MeP)  SeP SeP | модус celarent |
| (SaP  SiP) SiP)  (PaS (PaS  PiS) PiS) | |
| (SaP  SiP) SiP)  SaS SaS | |
| (SaP  StP) StP)  SaS SaS | |
| (SaP  StP) StP)  (PaS (PaS  PtS) PtS) | |
| (SaS&¬PaP) SeP SeP | |
| (SaS & SeP´)  SaP SaP | |
| (SeM & MeP)  SaP SaP | |
| (SeP & PiP & PoP)  SeS SeS | |
| (SiM & MaP)  SiP SiP | |
| (SiM & MiP)  SiP SiP | |
| (SoP & SiS)  SiP´ SiP´ | |
| (SuM & MaP)  SuP SuP | |
| (SuM & MaP)  SuP SuP | |
| (a<b & b<c)  a<c a<c | транзитивность строгого порядка |
| (a=b & b=c)  a=c a=c | транзитивность равенства |
| (vaS & vaP)  SiP SiP | |
| (v S & SaP) S & SaP)  v v P P | |
| (v S & v S & v P) P)  SiP SiP | |
| (vaM & MaP)  vaP vaP | |
|  ( ( A&A A&A B) B)   ( ( B&B B&B A) A) | модальная аксиома 3 |
|  (A (A B) B) ( ( A A  B) B) | модальная аксиома K |
|  A A | модальная аксиома V, или Ver |
|  A A   A A | модальная аксиома 4 |
|  A A  A A | модальная аксиома D |
|  A A A A | модальная аксиома T |
|  (A& (A& B) B)   (A (A   B) B) | модальная аксиома 2 |
|  A A  ¬ ¬ ¬A ¬A | связь сильной и слабой модальностей |
|  A A  A A | модальная аксиома Triv |
|  A A  A A | модальная аксиома Tc |
|  A A   A A | модальная аксиома 5 |
| 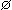 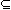 P P | |
|  x( x( yCxy yCxy   zTzx) & zTzx) &  x( x( yTxy yTxy   zCzx) zCzx) | формализация аксиомы Спинозы: Из данной определенной причины необходимо вытекает действие, и наоборот, – если нет никакой определенной причины, невозможно, чтобы последовало действие |
|  x(A x(A  B) B)  (A (A   xB), если A не содержит свободных вхождений x xB), если A не содержит свободных вхождений x | |
|  x(Cxx x(Cxx  Nx) Nx) | формализация определения Спинозы: Per causam sui intelligo id, cujus essentia involvit existentiam; sive id, cujus natura non potest concipi nisi existens (Под причиною самого себя я разумею то, сущность чего заключает в себе существование, иными словами, то, чья природа может быть представляема не иначе: как существующею) |
|  x(Dxx x(Dxx  Cxx) Cxx) | экспликация пресуппозиции Спинозы: x зависит от самого себя е.т.е. x - причина самого себя |
|  x(Ex x(Ex  Nx) Nx) | формализация определения Спинозы: Под вечностью я понимаю самое существование, поскольку оно представляется необходимо вытекающим из простого определения вечной вещи |
|  x(Gx x(Gx  (Sx & Hx)) (Sx & Hx)) | формализация определения Спинозы: Per Deum intelligo ens absolute infinum, hoc est, substantiam constantem infinitis attributus, quorum unumquodque aeter-nam, et infinitam essentiam exprimit (Под Богом я разумею существо абсолютно бесконечное, т.е. субстанцию, состоящую из бесконечно многих атрибутов, из которых каждый выражает вечную и бесконечную сущность) |
|  x(Ixx x(Ixx   y(¬x=y & Ixy)) y(¬x=y & Ixy)) | формализация аксиомы Спинозы: Все, что существует, существует или само в себе, или в чем-то другом |
|  x(Kx x(Kx   y(Kxy & Lyx & ¬x=y)) y(Kxy & Lyx & ¬x=y)) | формализация определения Спинозы: Ea res dicitur in suo genere finita, quae alia ejusdem narurae terminari potest. Ex. gr. corpus dicitur finitum, quia aliud semper majus concipimus. Sic cogitatio alia cogitatione terminatur. At corpus non terminatur cogitatine, nec cogitatio corpore (Конечною в своем роде называется такая вещь, которая может быть ограничена другой вещью той же природы. Так, например, тело называется конечным, потому что мы всегда представляем другое тело, еще большее. Точно так же мысль ограничивается другой мыслью. Но тело не ограничивается мыслью, и мысль не ограничивается телом) |
|  x(Nx x(Nx   y(Eyx y(Eyx   z(Azy z(Azy   u(z=u)))) u(z=u)))) | формализация аксиомы Спинозы: Сущность всего того, что может быть представляемо не существующим, не заключает в себе существования |
|  x(Qx x(Qx  ¬ ¬ yLyx) yLyx) | экспликация пресуппозиции Спинозы: Что-либо является свободным е.т.е. его ничто не ограничивает |
|  x(Qx x(Qx  (Nx & Cxx)) (Nx & Cxx)) | формализация определения Спинозы: Свободной называется такая вещь, которая существует по одной только необходимости своей собственной природы и определяется к действию только сама собой. Необходимой же или, лучше сказать, принужденной называется такая, которая чем-либо иным определяется к существованию и действию по известному и определенному образу |
|  x(Sx x(Sx  Dxx) Dxx) | одна из трех аксиом, формализующих третее определение Спинозы: Per substantiam intelligo id, quod in se est, et per se concipitur: hoc est id, cujus conceptus non indiget conceptu alterius rei, a quo formari debeat (Под субстанцией я разумею то, что существует само в себе и представляется само через себя, т.е. то, представление чего не нуждается в представлении другой вещи, из которой оно должно было бы образоваться) |
|  x(Sx x(Sx  Ixx) Ixx) | одна из трех аксиом, формализующих третее определение Спинозы: Per substantiam intelligo id, quod in se est, et per se concipitur: hoc est id, cujus conceptus non indiget conceptu alterius rei, a quo formari debeat (Под субстанцией я разумею то, что существует само в себе и представляется само через себя, т.е. то, представление чего не нуждается в представлении другой вещи, из которой оно должно было бы образоваться) |
|  x(Sx x(Sx  ¬ ¬  y (Dxy & ¬y=x)) y (Dxy & ¬y=x)) | одна из трех аксиом, формализующих третее определение Спинозы: Per substantiam intelligo id, quod in se est, et per se concipitur: hoc est id, cujus conceptus non indiget conceptu alterius rei, a quo formari debeat (Под субстанцией я разумею то, что существует само в себе и представляется само через себя, т.е. то, представление чего не нуждается в представлении другой вещи, из которой оно должно было бы образоваться) |
|  x(x=x) x(x=x) | рефлексивность равенства |
|  x x y(Sx y(Sx  Ayx) Ayx) | одна из двух аксиом, формализующих четвертое определение Спинозы: Per attributum intelligo id, quod intellectus de substantia percipit, tanquam ejusdem essentiam constituens (Под атрибутом я разумею то, что ум представляет в субстанции как составляющее ее сущность) |
|  x x y(¬ y(¬ zWxyz zWxyz  ( ( v(Uvx & ¬Uvy) & v(Uvx & ¬Uvy) &  v(Uvy & ¬Uvx) & ¬Dxy & ¬Dyx)) v(Uvy & ¬Uvx) & ¬Dxy & ¬Dyx)) | формализация аксиомы Спинозы: Вещи, не имеющие между собой ничего общего, не могут быть и познаваемы одна через другую; иными словами - представление одной не заключает в себе представления другой |
|  x x y((¬x=y & ¬Dxy) y((¬x=y & ¬Dxy)  Dxx) Dxx) | формализация аксиомы Спинозы: Что не может быть представляемо через другое, должно быть представляемо само через себя |
|  x x y((¬x=y & Dxy) y((¬x=y & Dxy)  Pyx) Pyx) | экспликация пресуппозиции Спинозы: Если x и y различны и x зависит от y, то y первее x |
|  x x y((Dxy y((Dxy  Dyx) Dyx)   wWxyw) wWxyw) | экспликация пресуппозиции Спинозы: x зависит от y или y зависит от x е.т.е. x и y имеют что-либо общее |
|  x x y(Axy y(Axy  (Sy & Exy)) (Sy & Exy)) | одна из двух аксиом, формализующих четвертое определение Спинозы: Per attributum intelligo id, quod intellectus de substantia percipit, tanquam ejusdem essentiam constituens (Под атрибутом я разумею то, что ум представляет в субстанции как составляющее ее сущность) |
|  x x y(Cxy y(Cxy   z(Uzy z(Uzy  Uzx)) Uzx)) | формализация аксиомы Спинозы: Знание действия зависит от знания причины и заключает в себе последнее |
|  x x y(Mxy y(Mxy  (Sy & Ixy & ¬x=y & Dxy)) (Sy & Ixy & ¬x=y & Dxy)) | формализация определения Спинозы: Per modum intelligo substantiae affectiones, sive id, quod in alio est, per quod etiam concipitur (Под модусом я разумею состояние субстанции, иными словами, то, что существует в другом и представляется через другое) |
|  x x y(x<y y(x<y  ¬y<x) ¬y<x) | антисимметричность строгого порядка |
|  x x y(x=y y(x=y  ¬x<y) ¬x<y) | несовместимость равенства и строгого порядка |
|  x x y(x=y y(x=y  y=x) y=x) | симметричность равенства |
|  x x y y u u v((Eux & Evy) v((Eux & Evy)  (x=y (x=y  u=v)) u=v)) | экспликация пресуппозиции Спинозы: Если u - сущность x и v - сущность y, то x=y е.т.е. u=v |
|  x x y y z(x<y & y<z z(x<y & y<z  x<z) x<z) | транзитивность строгого порядка |
|  x x y y z(x=y & y=z z(x=y & y=z  x=z) x=z) | транзитивность равенства |
|  xA(x) xA(x)  A(t), если не одна переменная из терма t не оказывается связанной в результате такой подстановки A(t), если не одна переменная из терма t не оказывается связанной в результате такой подстановки | |
| A   xA xA | принцип обобщения (генерализация) |
| A&¬A | противоречие |
| A (A (A B) B) | введение дизъюнкции |
| A (B (B (A&B)) (A&B)) | введение конъюнкции |
| A (B (B A) A) | закон утверждения консеквента |
| A   A A | модальная аксиома B, Br |
| A A A | закон тождества |
| B (A (A B) B) | введение дизъюнкции |
| C ((A ((A B) B) (A (A B)) B)) | |
| MaS MaP MaP | |
| Me(S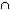 P)´ P)´  (MeS´ & MeP´) (MeS´ & MeP´) | |
| Me(S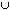 P) P)  (MeS & MeP) (MeS & MeP) | |
| P´´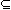 P P | |
| PaP (SeP (SeP PeS) PeS) | |
| S´´aP SaP SaP | |
| S´´aS | |
| S P P  S S S S | |
| S P P  SaP SaP | |
| S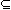 P P  (S (S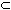 P P  S=P) S=P) | определение нестрогого включения через равенство и строгое включение |
| S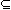 P´ P´  P P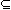 S´ S´ | |
| S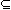 S S | рефлексивность нестрогого включения |
| S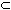 P P  ¬P ¬P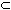 S S | антисимметричность строгого включения |
| S=P  ¬S ¬S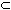 P P | несовместимость равенства и строгого включения |
| S=P  P=S P=S | симметричность равенства |
| S=S | рефлексивность равенства |
| SaP | |
| SaP  PaP PaP | |
| SaP  SaS SaS | |
| SaP´´ SaP SaP | |
| SaP´  (SeP & SiS) (SeP & SiS) | |
| SaP  SeP SeP  SiP SiP | |
| SaP  SeP SeP  StP StP | |
| SaP  (SeP´ & SiS) (SeP´ & SiS) | |
| SaP  SeP´ SeP´ | |
| SaP  ¬SeP ¬SeP | контрарность высказываний типа A и E |
| SaP  ¬SiP ¬SiP | |
| SaP  ¬StP ¬StP | |
| SaP  (SaS & PaP) (SaS & PaP) | |
| SaP  PaS PaS | |
| SaP  SeP´ SeP´ | |
| SaP  SiP SiP | закон подчинения |
| SaP  SiS SiS | |
| SaP  SqP SqP | |
| SaP SiS SiS | |
| SaP (SiP&SeP´) (SiP&SeP´) | |
| SaP P´aS´ P´aS´ | |
| SaS | закон силлогистического тождества для A |
| SaS´´ | |
| SaS´ SaP SaP | |
| SaS  (SaP (SaP  SeP SeP  SiP) SiP) | |
| SaS  (SaP (SaP  SeP SeP  StP) StP) | |
| SeM (PeM´ (PeM´ SeP) SeP) | |
| SeM (PiM (PiM S´iP) S´iP) | |
| SeP | |
| SeP  ¬SiP ¬SiP | контрадикторность высказываний типа E и I |
| SeP  SaS SaS | |
| SeP  (¬SiP & SiS) (¬SiP & SiS) | |
| SeP  ¬SiP ¬SiP | |
| SeP  ¬StP ¬StP | |
| SeP  PeS PeS | закон обращения E |
| SeS  SaS SaS | |
| SeS  SaP SaP | |
| SeS  SeP SeP | |
| SeS´ | |
| SiP | |
| SiP  SiP´´ SiP´´ | |
| SiP  (S (S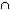 P)aP P)aP | |
| SiP  (S (S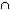 P)aS P)aS | |
| SiP  PiS PiS | закон обращения I |
| SiP  SaP SaP | |
| SiP  SiS SiS | |
| SiP SaS SaS | |
| SiP ¬SeP ¬SeP | |
| SiP SaS SaS | |
| SiS  S´iS´ S´iS´ | |
| SiS  SqS SqS | |
| SiS  SaS SaS | |
| SiS SaU SaU | |
| SoP  (¬SaP & SiS) (¬SaP & SiS) | |
| SoP  ¬SaP ¬SaP | контрадикторность высказываний типа A и O |
| SoP  ¬SaP ¬SaP | |
| SoP  PqP PqP | |
| SoP  SiS SiS | |
| SoP (SeP (SeP SiP´) SiP´) | |
| SoP SiP´ SiP´ | |
| SoS´ | |
| SqP  ¬SuP ¬SuP | |
| SqP  SaS SaS | |
| SqP  SqS SqS | |
| SqS | |
| SuP  PuS PuS | |
| a<b  ¬b<a ¬b<a | антирефлексивность строгого порядка |
| a=a | рефлексивность равенства |
| a=b  ¬a<b ¬a<b | несовместимость равенства и строгого порядка |
| a=b  b=a b=a | симметричность равенства |
| f A A | закон противоречия |
| t | |
| uS  PaS PaS | |
| uS  SiS SiS | |
| v´iv´ | |
| vaw  wav wav | |
| v S S  (v (v P P  v v P´) P´) | |
| v S S  vyS´ vyS´ | |
| vav | |
| veS  vaS´ vaS´ | |
| vyS  ¬v ¬v S S | |
| vyS  v v S´ S´ | |
| Схемы аксиом интуиционистской логики высказываний | введено для сокращения описания прикладных теорий, см. определение теории H |
| Схемы аксиом классической логики высказываний | введено для сокращения описания прикладных теорий, см. определение теории TV |
| Схемы аксиом классической логики предикатов | введено для сокращения описания прикладных теорий, см. определение теории QTV |
| Схемы аксиом теории THcie+ | введено для сокращения описания прикладных теорий. Существует описание только с правилами вывода. Для формулировки с аксиомами необходимы дальнейшие исследования. |